Harmonic Overtones Lab

Method and Results:

Using a Pasco Variable Wave Driver and a Pasco Student Function Generator standing waves were created of known frequency on a string (f).  

The other end of the string was attached to a pulley and weighed down with known mass (M).  This mass (M) was multiplied by gravity to determine the tension on the string (T).  The total length of the string was measured (L) and the amount of nodes, (n), created in the standing wave were recorded with respect to frequency.  

The mass of the string was recorded and divided by its length to determine the mass per unit length (m).  This information was used to determine the wavelength of the wave at certain frequency. 

frequency	muew	Tension	nodes	Velocity	Wavelength
16.0	1.88E-03	1.95902	2	37.5565	2.35
32.0	1.88E-03	1.95902	3	37.5565	1.17
46.0	1.88E-03	1.95902	4	37.5565	0.816
63.0	1.88E-03	1.95902	5	37.5565	0.596
76.0	1.88E-03	1.95902	6	37.5565	0.494
109.0	1.88E-03	1.95902	8	37.5565	0.345
frequency	muew	Tension	nodes	Velocity	Wavelength
27.0	1.88E-03	0.98196	2	22.8543	0.846
32.0	1.88E-03	0.98196	4	22.8543	0.714
54.0	1.88E-03	0.98196	6	22.8543	0.423
frequency	muew	Tension	nodes	Velocity	Wavelength
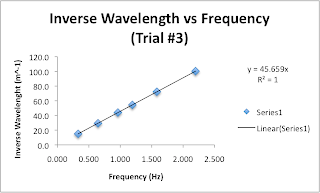
15.0	1.88E-03	3.92	2	45.663	3.04
29.4	1.88E-03	3.92	3	45.663	1.55
44.0	1.88E-03	3.92	4	45.663	1.04
54.4	1.88E-03	3.92	5	45.663	0.839
72.3	1.88E-03	3.92	6	45.663	0.632
100.3	1.88E-03	3.92	7	45.663	0.455

Conclusion: 

All data obtained was graphed and these graphs produced perfect linear equations when the inverse wavelength was taken and plotter with respect to the frequency. 

The slopes of each of these lines are the velocities of the waves on their respective strings.   When using a string with the same mass per length the frequency to obtain the same harmonic in different trials is directly proportional to the hanging mass used.